The Inner Product, August 2003
Jonathan Blow (jon@number-none.com)
Last updated 12 January 2004

Arithmetic Coding, Part 1

Related articles:
Arithmetic Coding, Part 2 (September 2003)
Adaptive Compression Across Unreliable Networks (October 2003)
Piecewise Linear Data Models (November 2003)
Packing Integers (May 2002)
Scalar Quantization (June 2002)
Transmitting Vectors (July 2002)

The Arithmetic Coder

When creating a networked game, we need to transmit messages between a client and server, or between peers. Bandwidth is expensive on the server side and perhaps scarce on the client side; therefore we want our messages to be as small as possible, while containing as much information as possible. In other words, we want those messages to be compressed.

At present, most games do not do a good job of compression, even games that spend a lot of money for bandwidth and would benefit hugely from such compression. Often, games will compose network messages using values that are multiples of a byte in size; more ambitious games will trim their values down to a 1-bit resolution using something like the Bit Packer I discussed last year ("Packing Integers", The Inner Product, May 2002). But as I pointed out in that article, a 1-bit resolution still wastes significant bandwidth when your values are small. I introduced the Multiplication Packer as a simple way to pack values without wasting space.

Back then I only discussed packing, which is just one part of compression. Statistical modeling is the other part: if data contains some values that are more common than others, we can exploit that fact to reduce the overall size. That's where the Arithmetic Coder comes in. You can think of the arithmetic coder as a more complex version of the Multiplication Packer that allows you to compose large messages and to use statistical modeling to crunch those messages into a small space.

This month I'll provide some engineering reasons you want to use an arithmetic coder; I'll also talk about packing values in the absence of any statistical modeling. We'll do modeling next month.

Engineering Reasons to Use an Arithmetic Coder

The arithmetic coder is a plug-in replacement for the bit packer or other buffering scheme that your game already needs. I've found my engine gets simpler when I switch to an arithmetic coder, due tothe coder's elegance. I also gain confidence in the engine's solidity, since it becomes impossible to have range-checking problems. Briefly, I'll explain the reason range-checking is necessary with a bit- or byte-packer.

Someone who's attacking your system, or perhaps just a fouled-up packet transmission, can cause your game to receive a message filled with garbage values. Therefore you can't trust any value you read from a network message. Specifically, suppose you are unpacking a 4-byte value that indicates the length of some array. You might know that a legitimate client will never pack a value higher than 5000, which you chose as the maximum array length. But if you read the 4-byte quantity without range-checking it, and it consists of garbage data, you could get a number in the billions. Subsequently attempting to allocate a billion-element array will cause you problems.

This basic phenomenon is the source of much grief in networked games. As a recent example, the Unreal engine was shown to exhibit this problem in several ways; all networked games built on the engine were affected. (See the References). The problem isn't restricted to the case of 4-byte array lengths; range-checking is also necessary for smaller values, say, 4 bits wide.

For today's discussion, the basic API for packing a value into a message looks like this:

void Arithmetic_Coder::pack(int value, int maximum_value);
int Arithmetic_Coder::unpack(int maximum_value);

Suppose that somewhere in my code I have defined:

const int ARRAY_LENGTH_MAX = 5000;
extern Arithmetic_Coder *coder;
extern Array array;

If you want to put the length of an array into the current message, you do this:

coder->pack(array.length, ARRAY_LENGTH_MAX);

The coder is probably written to assert if you pass a 'value' parameter that exceeds the 'maximum_value'. When the guy receiving the message wants to get the length back out, he does this:

int length = coder->unpack(ARRAY_LENGTH_MAX);

At this point, 'length' will always be between 0 and ARRAY_LENGTH_MAX. So long as you've defined ARRAY_LENGTH_MAX appropriately, you can't obtain horrible results. Garbage input will just give you a garbage value within the legitimate range. (Though you may wish to somehow detect garbage packets, it is now unlikely that improper detection will cause your game to crash).

Once the arithmetic coder is in place, you can start feeding it probability tables that describe the input data, and your bandwidth usage will magically go down. Generating these tables does take a little bit of effort, but the nice thing is that they are not required. If you're prototyping, or you don't care about certain message types, you just don't supply tables for them. You only compute the tables you need, and you don't bother with that until bandwidth conservation becomes a high priority. This is all nice and ideal!

It should be standard practice for networked games to use an arithmetic coder. Despite all the benefits, though, I'm not aware of a single game that uses a full-blown arithmetic coder for networking. That's a tragedy. (I'm using one in my current project, but it's not done yet so it doesn't count!)

How an Arithmetic Coder Works; Relation to the Multiplation_Packer

Lots of references out there will tell you various mechanisms for implementing an arithmetic coder; see for example the paper by Howard and Vitter (see References). I don't want to flog that horse, so I'm hoping you'll read some references. Here I'll look at the coder from an untraditional viewpoint, and try to supply some less easily-found intuition about _why_ it works.

Recall the basic functionality of the Multiplication Packer, shown in Listing 1.

(Listing 1):

Multiplication_Packer::Multiplication_Packer() {
    accumulator = 0;
    range = 1;
}

void Multiplication_Packer::pack(u32 value, u32 limit) {
    range *= limit;
    accumulator = (limit * accumulator) + value;
}

You call 'pack' repeatedly to create a message. When you're done, you have an integer between 0 and range-1, which you somehow put into a network packet. Back then we used the Bit_Packer to do this; the magnitude of 'range' tells us how many bits we need. You can visualize the packing operation as indexing a 2D grid, as in Figure 1. See last year's article for more detail.

The multiplication packer was somewhat inconvenient; you can see that every time you pack a value, 'range' gets larger. If you try to pack too much, the packer overflows the 32-bit integer and you're in trouble. We would like to somehow spool the data into a buffer as we pack, to prevent overflow and eliminate the cumbersome use of a separate Bit Packer. Unfortunately it's unclear how to do this; since all the bits of 'range' change every time you multiply, there seems to be nothing coherent to store in such a buffer.

The arithmetic coder gets around this using a simple but effective trick: instead of packing an integer between 0 and range-1, we're going to pack a fixed-point binary number between 0 and 1. With the multiplication packer we add information to a number by letting its magnitude grow divergently -- now, instead, we will add information by growing the number to the right of the decimal, in a way such that it converges toward a limit. Because the number converges quickly, some of its most significant bits become stable after each packing step; those stable bits can be written into a buffer, freeing up space within the 32-bit integer.

It's astonishing how easy it is to make this change when playing with the math. The multiplication packer gives us a number in the interval [0, range) and we want a number in [0, 1) so we just divide by 'range'.

If we write out the function of the multiplication packer as a recursive rule, we get this:

After n total packing steps, range will be:

Now I am going to rewrite the equation for accum_n by expanding the definition of accum_n-1:

We can repeat this expansion recursively, rewriting the term for accum_n-2 and so on. I'll do it just once more:

We refactor this equation by distributing the multiplication across the addition:

Now an interesting pattern starts to become clear. But the above equation still isn't fully expanded, because we have that accum_n-3 term that we could keep expanding all the way down to accum_1. Let's do that:

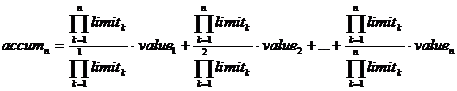Recall that I am doing all this because I want to divide by (range_n = PI(n) limit). And looking at the equation now, it's trivial. This equation really wants to be divided by PI(n) limit. It's _begging_ for it. So:

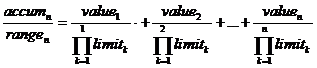The terms of this sequence converge, because the denominator grows geometrically but the numerator doesn't in general grow. The result is the value between 0 and 1 computed by an arithmetic coder. To reiterate, it's the value computed by the multiplication packer, divided by range_n. This divide allows us to incrementally save out the most significant bits of the result, achieving successful packing of arbitrarily many values.

To me, the grid-ness of the multiplication packer is easy to visualize, but the shrinky-ness of the arithmetic coder is less so. Being able to factor between them gives me comfort.

The actual implementation of an arithmetic coder looks somewhat different from the multiplication packer; but you can see from the math that they're close relatives. We'll talk about specific implementation trade-offs next month; for now you can look at the sample code, which illustrates a bare-bones arithmetic coder.

A Tangential Rant about Online Security

As I write this, one of the big news items is that the game Shadowbane, developed by Wolfpack and published by Ubi Soft, has been hacked in a highly amusing way. A group of players managed to grant themselves game master priveleges; they proceeded to summon huge nasty monsters into safe zones to kill other players, and to teleport everyone down to the bottom of the sea for further carnage (see the References).

In this case, it was clear that Wolfpack had placed far too much authority in the client side of their software. They had failed to heed the number one rule of client/server system design: "The client is in the hands of the enemy." (See Jessica Mulligan's article in the References). Yet no sooner had the hack occurred than Ubi Soft released a statement promising legal prosecution of the hackers. I hope no such persecution comes to pass; it's ridiculous to sue someone for your own disregard of sound engineering practices.

Since security is such an important topic, I'll now discuss how arithmetic coders affect security. This is a more involved topic than Shadowbane's specific problem; but I bring up Shadowbane because it's a clear illustration that, as Jessica laments, online game developers keep making the same mistakes. But if we raise the general level of design consciousness vis-a-vis security, we can develop standard architectures that preclude these mistakes.

Arithmetic Coders and Security

As we've seen, when we use an arithmetic coder to pack up messages, individual data items get multiplied by arbitrary values before they are written into the output buffer. To a casual viewer -- someone looking at your network transmissions with a packet sniffer or a hex editor -- the data will appear unstructured, since important fields will tend not to land on bit boundaries. Since your game protocol is difficult to see, it is difficult to hack.

This statement is more than anecdotal when you look at the situation from an information-theoretic viewpoint. Compression works by exploiting and reducing predictable structure. This increases the "entropy" of the data. Data with no structure whatsoever is random and has maximum entropy. Thus, perfectly compressed data appears completely random.

This idea of maximum entropy comes up in another area we're familiar with: encryption. Like compression, encryption is about crunching on data in a reversible way to produce maximum-entropy output. So in a sense, perfect compression is equivalent to perfect encryption; the probability tables act as a secret key.

Unfortunately, our current compression schemes are nowhere near perfect, so data that's "encrypted" via compression is very crackable. Even high-order statistical models of the input data will leave a lot of structure in the output. So you should not use just an arithmetic coder to encode life-or-death secrets and then consider them secure. But the point I wish to make is, when you use an arithmetic coder hacking your protocol becomes a matter of employing statistical analysis, known-plaintext attacks, etc. Either that, or reverse-engineering all your networking from assembly language. Both of these options require substantial effort on the part of a would-be hacker; most of the people with enough knowledge to hack your protocol will be off programming their own games.

So just by using an arithmetic coder, with our primary goal being to save bandwidth, we also raise the barrier to entry for those who want to hack our game. That's a nice side-benefit.

Now suppose you do really want to secure your data stream. You should use a hard encryption algorithm for this. But even in that case, the arithmetic coder helps you out. The reason is that hard cryptographic algorithms become easier to brute-force attack the more you know about the input data. Suppose a hacker is playing your game and he types a chat message; this causes an encrypted network packet to be sent to the server. He knows that the source data is mostly ASCII text, and he can use this knowledge to help break the encryption key. But if you compress the data with an arithmetic coder prior to encyrption, the hacker must work a lot harder to break the key. For more of an explanation of this, and some other benefits of using compression to precondition data before encryption, see section 8.5 of the sci.crypt FAQ (see References).

Charles Bloom has pointed out to me that the preceding discussion is slightly dangerous, since there have been several attempts to use arithmetic coders as strong encryption, but all such systems have been shown to be breakable. So I want to re-emphasize that I am not encouraging the use of such schemes. If you need strong encryption, use a strong encryption algorithm. If you don't need strong encryption, you can still take comfort in the fact that, by compressing your data, you've gained protection against the casual intruder.

References

Paul G. Howard and Jeffrey Scott Vitter, "Practical Implementations of Arithmetic Coding", http://citeseer.nj.nec.com/howard92practical.html

MACM-96 Arithmetic Coder, http://www.cbloom.com/news/macm.html

Cryptography FAQ for sci.crypt, section 8.5: "How do I use compression with encryption?", http://www.faqs.org/faqs/cryptography-faq/part08/

Auriemma Luigi, summary of Unreal network security bugs. http://www.pivx.com/luigi/adv/ueng-adv.txt

Background info and discussion on Shadowbane hacks: http://games.slashdot.org/games/03/05/28/1452201.shtml

Jessica Mulligan, "EULAQuest: Part Two", Biting the Hand Volume 9, Issue 13, May 4, 2000. http://www.skotos.net/articles/BTHarchives/BTH2000.pdf