The Inner Product, September 2003
Jonathan Blow (jon@number-none.com)
Last updated 12 January 2004

Related articles:
Arithmetic Coding, Part 1 (August 2003)
Adaptive Compression Across Unreliable Networks (October 2003)
Piecewise Linear Data Models (November 2003)
Packing Integers (May 2002)
Scalar Quantization (June 2002)
Transmitting Vectors (July 2002)

Say we’ve got a client/server game system. We want to transmit as much data as we can through a limited amount of bandwidth; an example of such data would be the server telling the client the states of all objects in the world. Last month, we saw how an arithmetic coder can help us efficiently pack data values into network messages, at sub-bit precision. This meant there were no gaps between the individual values, which saved space, especially when values were small.

But if we want bigger space savings, the thought occurs that we can outright compress the transmitted data. We might do this by a relatively brute-force approach, such as linking the free ‘zlib’ compression library into our game, passing it our network messages as arrays of bytes, and telling it to compress those arrays. There are a lot of reasons why this isn’t a good idea, some of which will become clear as we discuss alternatives today.

Arithmetic coders are great at compression. Once again I am going to refer you to some excellent references, like the CACM87 paper, to explain the basics of arithmetic coding compression (see References). Here I'll try to provide some alternative views not found in the references. I'll also discuss ways we, as game programmers, need to approach arithmetic coding differently from the mainstream.

Just like last month, we encode a message by mapping it to a small piece of the interval [0, 1). Compression occurs by transforming values so that common values take up large pieces of the interval, and rare values take small pieces. The ideal amount of space that any value or message can be compressed into is –log₂(p) bits, where p is the probability of that message. Don’t be confused by that minus sign; since p is always in [0, 1] by definition (it’s a probability!), the log always produces a result that is negative or zero, and the minus sign just reverses that. In Figure 1, I’ve tried to illustrate why it takes fewer bits to encode a bigger subset of the unit interval. You can think of the active principle as: "the smaller something is, the more precisely you must describe its location in order to guide someone to it".

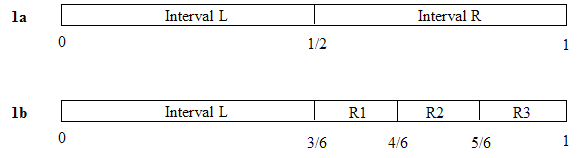
Figure 1 1a: The unit interval divided into two equal pieces, spanning [0, 1/2) and [1/2, 1).  To specify one of these pieces, we only need one digit after the point.  Binary .0 (0 decimal) indicates interval L, since any number starting with .0 lands in the range [0, ½).  Likewise, .1 is sufficient to denote R, since any number starting with .1 lands inside R. 1b: Interval R has been subdivided.  The number .0 is still sufficient to specify L.  However, .1 now could indicate any of the three intervals on the right; we need more digits to specify which.

We start with the interval [0, 1); for each value we want to pack, we pick a fraction of the current coding interval that’s equal to that value’s probability, and shrink the coding interval to that new subset. Last month, in order to pack a value into a message, given n possibilities for the value, we would just subdivide the current coding interval by n. That’s the same as treating all the possibilities as though they were of equal probabilities. So essentially, this month we’re just improving our model of the data’s statistics.

In Figure 2, I’ve drawn two different illustrations of this process of encoding a string of values. Figure 2a shows the recursiveness of the concept, showing how we zoom in on one tiny piece of the unit interval. Figure 2b takes a more aloof viewpoint, looking at the set of all possible messages we could transmit, and their relative probabilities. It’s a little more cluttered, but it’s useful because it helps clarify some aspects of message probabilities.

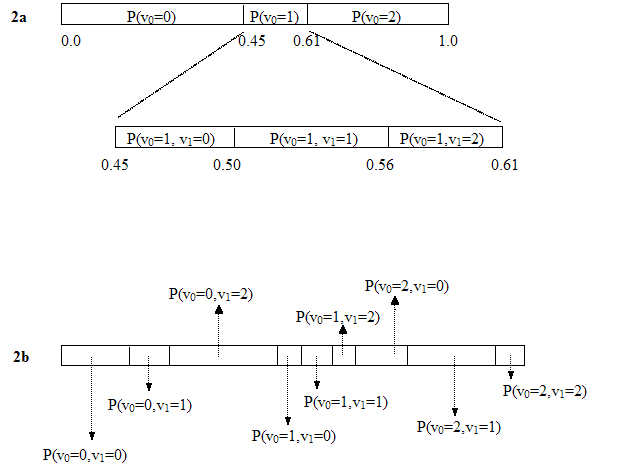
Figure 2: Suppose we create a message by packing together two variables v0 and v1, each of which can take on the values 0, 1, or 2.  Figure 2a shows the process of finding the appropriate piece of the unit interval, for the case when v0=1.  Figure 2b shows a birds-eye view of all message possibilities.

To get the best compression, we want to look at the set of all possible messages we could transmit, and ensure that each of those messages maps to a piece of the unit interval of the exact size dictated by its probability. Our goal is to compute P(y₀ = k₀, y₁ = k_1, … , y_n = k_n), the probability of the final composite message. If the y_i are statistically independent, the compound probability just becomes the product P(y₀ = k₀)P(y₁ = k₁) … P(y_n = k_n), and the answer is simple to compute since we don’t need context around any single value. But this criterion of independence almost never holds. Instead there are dependencies in there. In fact, thinking of this probability as being a divisible and well-ordered thing is probably a mistake. Certainly, nothing in reality limits the dependencies to flowing forward along with our indices on y. For some particular problem, we might need to compute P(y₃ = k₃ | (y₅ = k₅, y₉ = k₉), … , y₁ = k₁), and that is still a tremendously simplistic way of looking at the problem.

I bring this up in such an annoying fashion because data modeling for arithmetic coders is usually explained in the way that text compression guys see the problem. In that paradigm we have a bunch of uniformly-sized symbols and we run through some example data to build tables giving us a 0^th order or 1^st order or n^th order model of the data, which we then use for compression, perhaps adaptively. I find this mode of thought limiting when it comes to approaching general problems. As an example, Claude Shannon, father of information theory, did a number of experiments to compute bounds on the actual information content of the English language. The results of these experiments can tell you approximately what compression ratio you’d get out of a very good compressor. Shannon found an upper bound of about 1.3 bits per character, and a lower bound of half that; these numbers are much lower than the ratios achieved by the current best compressors. (For some example compression statistics see Charles Bloom’s web page in the References). Evidently, given an AI that understood English as well as a human, you could use its predictions of upcoming text to build a much better compressor than we currently know how to make.

Such an AI would perform well because it contains much knowledge about the behavior of English. This is not strictly a model of the way letters tend to follow each other in text; it’s a deeper thing, a model of what the author of the text was trying to do by writing the text. Actually it’s even deeper than that; it’s a model of the kinds of ways people tend to behave, allowing us, upon encountering a text, to generate a more specific model of what the text is intended to achieve. Overall, I wish to make this point: any knowledge you can exploit to predict the probability of a message is fair game. It doesn’t have to be information actually contained in the message.

This month’s sample code is a file compressor. And to compress files, we will use … only information contained within the files. But this is all because the code’s written to be as simple as possible, to be easy to understand and build on. It provides two options for compression: order 0 modeling (no context around each character) and order 1 modeling (one character of previous context is used to guess the probability of the current character). The code reads from an example English text file, in order to build a static probability model for the expected data. It then uses that model to compress a different file.

Most arithmetic coding text compressors use adaptive modeling, but this one does not. Adaptive modeling is a method of modifying the probability tables to fit the file’s usage patterns, as pieces of the file go streaming by. The nice thing about this is that you don’t need to store any probability tables; you just start the encoder and decoder in a context where all values are equally probable, then you just let them go and adapt. Arithmetic coders are ideal for adaptive modeling, which is one reason why people like arithmetic coders so much.

Unfortunately, in a high-performance networked game, adaptive modeling is not as straightforward as it is for a file compressor. Because the probability tables are implicit, the decoder needs to see the entire stream transmitted by the encoder. But in a networked game, we need to drop network messages or process them out of order. An adaptive decoder could not do this, as its probability model would fall out of synch with the encoder’s, causing it to produce garbage.

Next month, we’ll look at a scheme for adaptive modeling in a client/server environment. But you may decide that the necessary complication is not worthwhile; if so, a static probability model will still work for you. And thus, one of the primary purposes of this month’s sample code is to provide a simple example of a static modeler.

Last month’s encoder used an integer divide once per packed value to compute the new coding interval. This month’s code uses a bit shift instead, so it’s faster in that sense. Because we’re multiplying probabilities, and those probabilities are necessarily approximate (because we must fit them into a piece of a machine word), we can ensure that they’re represented as fractions whose denominators are a known power of 2. Rounding the probabilities this way does distort them a little bit, resulting in a loss of compression efficiency; but that loss is so small as to be unnoticeable.

Now I’ll talk about some ways in which the data you really want to transmit will differ from the sample code.

Much real-game data will be hierarchical. For example, to represent a game entity, we may have one object class definition per entity type; if the server wants to tell the client about this entity, it must transmit all the fields of that class definition. Those fields might be { type = WIZARD, position = (x, y, z), angle = 1.12, health = 73 }. If we transmit two entities to the client, we make a message that looks like: [ WIZARD, (x1, y1, z1), angle1, health1, BARBARIAN, (x2, y2, z2), angle2, health2 ]. Modeling this data as a linear sequence would be a mistake, since it’s unlikely that the value of health1 is usefully correlated with the next value in the sequence, the entity type BARBARIAN. But we may wish to draw correlations between parallel fields (members of a party traveling together are probably near each other, and are probably facing nearly the same direction). And we may wish to draw correlations between certain data fields, and certain other protocol messages. Consider a "drink potion" protocol message. If a character has low health and high mana, and he drinks a potion, chances are good it’s a potion of healing and not a potion of mana. Or, perhaps characters located near town are usually drinking potions of speed, so that they can quickly leave the safe area and get to the fighting; but characters located out near the fighting are usually drinking potions of health and mana, and almost no potions of speed.

This talk of position correlations brings up an important issue. As discussed last year, positions are generally transmitted as tuples of integers. Suppose I am camping with a party, we are moving about healing each other and keeping watch for monsters. My current X position is 4155 out of 10000. (This is just an example, and is likely to be too low-res a position for use in a real game). Since I’m milling about, my next X position is likely to be near 4155, but it probably won’t be 4155 exactly. It might be 4156. But a generalized data modeler, written in the way of file compressors, would treat 4155 and 4156 as unrelated "symbols". Such an adaptive modeler, upon seeing the 4155, would increase the probability of 4155 coming again in the data stream; but implicitly, this decreases the probability of seeing 4156, thus hurting compression if I am moving at all.

Because we move through space continuously, spatial values are correlated. 4155 is highly correlated with 4156, because those points are spatially nearby. Thus when transmitting an X coordinate of 4155, an adaptive modeler should actually increase the subsequent probability of all X coordinates in the neighborhood, using a Gaussian centered at 4155. Actually, we’d ideally want to intercorrelate X, Y, and Z, keeping the resulting probabilities in a 3D grid; this is expensive, though, and independent 1D tables for each coordinate are almost as good in practice. (Though the higher the number of dimensions we work in, the worse this approximation becomes; so be hesitant when using it for a high-dimensional model! This is related to the fact that as n grows, the unit sphere in n dimensions contains decreasing amounts of space compared to the unit cube.)

I call this type of data a "coherent" value. Another example of a coherent value is health; if you are at full health, and you’re being attacked, probably your health will go down gradually. It’s much less probable to drop instantly from high health to 0 health.

As mentioned earlier, good compression is all about making accurate predictions. Predicting the change of continuous values over time has a history in online games; it’s often known as "dead reckoning". So as it happens, we want good dead reckoning not only to fill in the gaps between network messages, but to help encode and decode those messages too.

Khalid Sayood, Introduction to Data Compression 2nd Edition, Academic Press, 2000.

Mark Nelson, "Arithmetic Coding + Statistical Modeling = Data Compression", Dr. Dobb's Journal January-February 1991. Available at http://dogma.net/markn/articles/arith/part1.htm

Ian Witten, Radford Neal and John Clearly, "Arithmetic Coding for Data Compression" (the CACM87 paper); University of Calgary technical report 1986-238-12, http://pharos.cpsc.ucalgary.ca/Dienst/UI/2.0/Describe/ncstrl.ucalgary_cs/1986-238-12

Charles Bloom’s compression page, http://www.cbloom.com/src/index.html