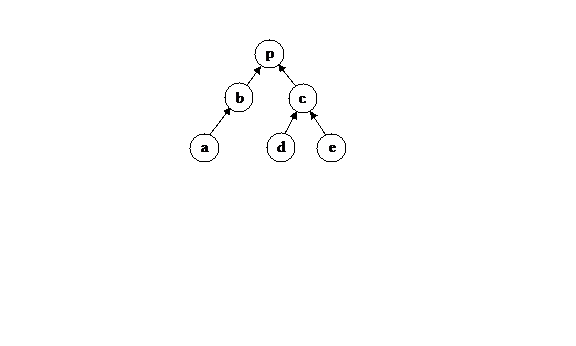
Figure 1: A set of nodes arranged in a tree. We represent this with the following set of predicate logic assertions: ['parent a b], ['parent b p], ['parent c p], ['parent d c], ['parent e c].
The Inner Product, March 2004
Jonathan Blow (jon@number-none.com)
Last updated 13 May 2004
Designing the Programming Language
"Lerp", Part 3
Related articles:
Predicate Logic (December 2003)
Lerp 1 (January 2004)
Lerp 2 (February 2004)
Lately, I’ve been developing a programming language called Lerp. Lerp is an imperative language with some declarative extensions for data handling. The declarative statements are in the form of Predicate Logic (see the December 2003 issue), a simple way of reasoning with facts that’s well-known in the AI community.
In the past few articles I’ve shown how the predicate logic
expressions can be used to manipulate data in concise and powerful ways.
However, the traditional handling of predicate expressions (in languages like
Prolog) has some problems that need to be addressed. Prolog was never adopted
into widespread use; I believe this is partially due to some clear software
engineering shortcomings that Prolog proponents have been slow to acknowledge
and fix.
Software engineering problems with traditional predicate logic
A language with “good software engineering properties” helps you keep a program from becoming too chaotic as it grows; such a language supports software development patterns that result in fewer bugs, and makes it easy to find bugs when they do happen. As an example, C++ performs type-checking at compile time and link time, so many common errors (like passing the wrong argument to a procedure) are caught and fixed before you ever run the program. On the other hand, Lisp doesn’t have static typechecking, so you can only find type errors at runtime. Those errors might lurk for a long time, if they’re in code paths that are infrequently exercised! So C++ provides a definite advantage over Lisp in terms of getting real work done.
On the whole, predicate logic is an error-prone method of expression. Traditionally there’s not much in the way of compile-time error checking. The speed of your program, and its correctness, depend drastically on small variations in the way the predicates are written. I’ll illustrate this with some examples.
Suppose you have some objects arranged in a tree; there is a relationship parent that links objects together (Figure 1). We want to ask whether one object is an ancestor of another, in other words, whether it can be reached by traversing some number of parent links. Using Lerp syntax, we would define the ancestor predicate like this:
[‘ancestor ?x ?a] <- [‘parent ?x ?a];
[‘ancestor ?x ?a] <- [‘parent ?x ?p] & [‘ancestor ?p ?a];
The first line says that a is an ancestor of x if a is the parent of x. The second line says: a is an ancestor of x if x has some parent p, and if a is an ancestor of p. This second line performs recursion and the first line handles the simplest case; the two lines together provide a complete definition of “ancestor”.
One of the nice aspects of predicate logic is supposed to be that it’s declarative; you just state the facts, and the runtime system just figures out the answers to your queries based on the facts. In reality, though, it’s just not that way. Facts don’t get up and solve problems by themselves; in predicate logic systems, there’s a solver algorithm that tries to put facts together to eliminate unknowns. The problem with traditional predicate logic systems is that, due to performance and correctness concerns, we end up spending most of our time thinking about the course of action this solver algorithm will take in order to put our facts together – when we’re supposed to be thinking just about the facts themselves.
For example, Prolog’s solver will consider the facts one by one in the order you list them. (For details, see the books in the References). The ancestor relation as I wrote it above would be an efficient way to write the program, but suppose you switch the order of the statements like this:
[‘ancestor ?x ?a] <- [‘parent ?x ?p] & [‘ancestor ?p ?a];
[‘ancestor ?x ?a] <- [‘parent ?x ?a];
Now you have a program that is extremely inefficient. It will always recurse first, climbing all the way to the root of the tree and whizzing right past the answer, only finding the answer as it backtracks.
The situation can get worse; suppose you switch the order of the conjunction in the first rule:
[‘ancestor ?x ?a] <- [‘ancestor ?p ?a] & [‘parent ?x ?p];
[‘ancestor ?x ?a] <- [‘parent ?x ?a];
Now the solver will just infinite-loop! An attempt to answer any “ancestor” question will cause the solver to immediately pose another “ancestor” question.
As long as our examples remain this simple, perhaps we can work around the problems without too much strife. Maybe we can add some compile-time checking to spot simple loops like the one above. But as with every language, the situation gets much murkier when the program gets bigger, as we add relations that reference each other recursively in various ways. As the program grows, we must work harder to manage the solver’s processing of the data. Writing a large-scale software project like this will not be as much about logic as one would hope.
To top it all off, there are a lot of places this kind of solver just can’t reach. Imagine that we want to make the solver navigate an arbitrary graph as in Figure 2. Here, we have a fact neighbor that tells us whether two nodes have an arc between them, and we want to define a relation connected that tells us whether two nodes are some number of neighbor-steps away. Well, a Prolog-style solver is just going to infinite-loop on this problem, period. In order to fix this, we need to add lots of extra data and relations in order to manage the solver’s progress, and we end up doing the same kind of work we must do in imperative language, except in a more Byzantine manner. Basically it just sucks. (Recent variants of Prolog, and other logic programming languages, apply various band-aid approaches to this problem, but I have not seen one that solves the problem to my satisfaction).
In such declarative languages, because flow control is
implicit, it’s very hard to deal with if you need to actually steer it. This is
not nearly as nice as in an imperative language, where the programs are lists of
statements that say “do this; then do this; then do this.”
Taking Control over the Solver
This straightforwardness of imperative languages is why I designed the core of Lerp to be imperative, but so far there’s an extreme asymmetry in the language design. The imperative part can scale, with reasonable confidence that the program will do what you think. The logic part, though, is only useful for simple tasks, because as facts in the logic system become more complicated, perhaps the program will start running slowly, or perhaps it will infinite loop, who knows really? I don’t feel like I can produce reliable programs within acceptable effort when things get large on the logic side.
Maybe that’s not so bad – if the imperative side is good
enough, maybe the language philosophy should be that logic is only used for
simple things. Certainly, the matrix and vector examples shown last month are
interesting and useful, and we could just accept those (along with the
carrying example) as the limit of what the logic in Lerp will do. But I
want to push it further.
Simplifying the Ancestor Definition
Throughout the language design process I have been keeping in mind the most effective features from other languages, like Perl, and looking for opportunities where they can be gainfully employed. In this case, I found a way to reframe Perl’s regular expression handling. Let’s go back and look at that definition of “ancestor”:
[‘ancestor ?x ?a] <- [‘parent ?x ?a];
[‘ancestor ?x ?a] <- [‘parent ?x ?p] & [‘ancestor ?p ?a];
What we’re trying to say here is “An ancestor is anyone you can reach by following a parent relation one or more times”. This is interesting because “one or more times” is a common, primitive concept in regular expression pattern matching: it’s denoted with a +. In fact, if we treat parent as a single symbol, then the idea “one or more parent relations” would just be written in regexp form as “parent+”. With that in mind we can develop an alternate syntax where ancestor is defined like this:
[‘ancestor ?x ?a] <- /{ ?x ‘parent+ ?a };
This definition treats the database facts of Figure 1 like a graph. The /{} are just syntactic markers saying that the braces contain instructions about how to walk the graph. This particular graph-walking expression says: start at x, then follow one or more parent arcs until you arrive at a. The symbol parent is still assumed to be a binary operator like in the previous definition. You can think of { ?x ‘parent+ ?a} as expanding to: [‘parent ?x ?tmp_1] & [‘parent ?tmp_1 ?tmp_2] & … & [‘parent ?tmp_n ?a].
If it helps reduce confusion, we can reformat the parent
facts in the database so that the identifier
‘parent is infix rather
than prefix, so the facts look like:
[node1 ‘parent node6] instead of
[‘parent node1 node6]. This is just a cosmetic
change, and clearly we can do a graph-walk among facts stored in either format.
More Complex Graph Walks
We can compose longer graph-walking expressions. Suppose we want to find whether x and y have a common parent. There are several ways we could form this query. We could say /{ ?x ‘parent+ ?p } & /{ ?y ‘parent+ ?p }, “Is there some common p reachable by parent-steps from both x and y?” Or if we define the relation child:
[‘child ?a ?b] <- [‘parent ?b ?a];
then we can string together one expression that looks like this: /{ ?x ‘parent+ ?p ‘child+ ?y }. That may be easier to think about since it talks about one continuous path, from x up to p and then down to y. But the point of child is just to define a transition that goes in the direction opposite of parent. Requiring a separate definition for that is a little cumbersome, though – instead, we can add some notation to the graph walking expressions to say “switch the order of the arguments before searching for this fact in the database.” Let’s use the ‘~’ character for this, the little wave symbolizing the swapping of two things. Then the query becomes: /{ ?x ‘parent+ ?p ~’parent+ ?y }; whether you prefer this is a matter of taste, but it does make for a simpler program. Another way to think of ~ is that it means “go backward along this graph edge instead of forward”.
Let’s apply this to a concrete game situation. Suppose you’re making a fantasy game, and a player who we will call victim has just been breathed on by a dragon. We want to apply damage_amount points of damage to everything that player is carrying, if it is flammable. We know an object is flammable if it has a member variable “flammable” that is set to true. The catch is, we need to search for items that are not in the player’s top-level inventory. If the victim is carrying a bag, and there’s a scroll in the bag, then we will have facts [‘carrying victim bag] and [‘carrying bag scroll], but probably no [‘carrying victim scroll] since such “deep linking” would make data handling cumbersome and expensive. So when it comes time to burn the stuff, we need to perform a recursive search through the player’s inventory to make sure we find everything. Supposing we have some function apply_damage, we can call it on all the relevant entities like this:
apply_damage(damage_amount, each /{ victim ‘carrying+ ?? .flammable });
In this graph walking expression, the “carrying+” finds all the entities starting from victim, the ?? indicates that the node in that slot should be the return value of the expression, and the “.flammable” looks up the member variable “flammable” on whatever value we reach. If that member variable doesn’t exist or is false, the traversal fails for that particular path and returns nothing; otherwise, it returns the node in the ?? slot. Recall that the “each” as a function argument causes apply_ damage to be called once for each entity that satisfies the query.
I think that’s pretty cool. It’s certainly different from what you’d do in most other languages, and it’s simpler. You can imagine ways of adding further regexp syntax to handle fireproof containers. It works out to be pretty simple. In fact most of the convenient features of regular expression syntax can be adopted directly into this graph-walking scheme (parentheses to join patterns into larger groups, etc).
What this notation does for us
This graph-walking syntax helps us phrase queries in more straightforward and compact ways than traditional predicate logic would allow. But it also does something more important: it gives us a way to avoid the recursion and termination pitfalls mentioned earlier in this article. When evaluating a term like carrying+, the graph walking engine can just assume some things that are difficult to deduce in a general predicate logic environment.
Going back to the non-hierarchical situation of Figure 2, a graph walker can easily solve the query with no danger of infinite-looping, without requiring the programmer to add ancillary data. It can just mark the nodes it’s visited and never try them again, since when evaluating a pattern option like +, there’s no reason to visit a node twice. This is valuable, since it widens the scope of queries that the programmer can make while feeling confident and safe. This month’s sample code implements the examples discussed here, and some others.
Relation to SNePS
The regular expression query syntax treats a predicate
logic database as a series of nodes connected by arcs. Interestingly, there are
some systems developed in the AI world that are centered around this idea of
graph traversal. The most prominent of these is SNePS (see References),
considered by some to be a helpful tool for knowledge representation in natural
language processing. The semantics of SNePS are not exactly like what we have
discussed here, though there are some interesting similarities.
References
Programming in Prolog, W.F. Clocksin, Springer-Verlag.
SNePS Research Group Home Page, http://www.cse.buffalo.edu/sneps/
|
Figure 1: A set of nodes arranged in a tree. We represent this with the following set of predicate logic assertions: ['parent a b], ['parent b p], ['parent c p], ['parent d c], ['parent e c].
|
|
Figure 2: A graph that contains cycles; this will cause problems for a Prolog-style solver. Each arc between the nodes represents an assertion of the form ['neighbor ?a ?b]. To ask whether a path exists between rooms, we may wish to define a primitive connected that traverses these neighbor facts.
|