The Inner Product, May 2003
Jonathan Blow (jon@number-none.com)
Last updated 16 January 2004
 

Unified Rendering Level-of-Detail, Part 3

Related articles:

Rendering Level-of-Detail Forecast (August 2002)
Unified Rendering LOD, Part 1 (March 2003)
Unified Rendering LOD, Part 2 (April 2003)
Unified Rendering LOD, Part 4 (June 2003)
Unified Rendering LOD, Part 5 (July 2003)

Figure 1a (upper left): A 10000-triangle tessellation of the Stanford Bunny.  Figure 1b (upper right): The bunny has been clipped in half with the halves joined together by a seam. We've moved the bunny halves artificially far apart to clearly show the seam. To make individual seam triangles distinct and obvious, the seam is drawn with garish colors. Figure 1c (lower left): The right half of the bunny has been passed through a detail reducer, decreasing its triangle count by a factor of 4. The seam has been cross-referenced and correctly preserves the manifold.  Figure 1d (lower right): The bunny halves, at differing LODs, have been moved back together and the seam is now drawn using the same shader as the rest of the bunny.

My goal so far has been to develop a general method of LOD management that works for a wide variety of geometry types. But so far I've only discussed the rendering of regularly sampled height fields. This month I'll start extending the system to triangle soups.  You can see the results in Figure 1.

Recall that the basic algorithm works by dividing the input data into spatially-localized blocks, then hierarchically combining those blocks. Because we were working with height fields, the vertices were spread mainly across two dimensions, so the array of blocks was two-dimensional. Since the input data was a grid of samples, dividing the data into blocks was easy, and building the initial seams between high-resolution blocks was also easy.

Now, we want to allow the triangle soup to extend arbitrarily in any direction, so the array of blocks must be three-dimensional. Building the blocks and seams will also be more involved. But fortunately, we're already familiar with the necessary tools; we use them when constructing spatial organizations in a variety of triangle-processing algorithms.


Clipping or Binning?

We want to divide the input geometry into a three-dimensional grid of blocks. Since the triangles will not generally be aligned with block boundaries, the obvious idea is to clip the geometry using planes aligned with the faces of each block.

However, the goal of dividing the geometry into blocks was just to create groups of triangles, where each triangle is located near the other triangles in its group. Strictly speaking, there is no algorithmic requirement that prevents the blocks' bounding volumes from overlapping. So instead of clipping, we could divide the geometry as follows: (1) start with a set of empty "bins", each representing a cubic area of space; (2) for each input triangle, find the cube that contains its barycenter, and put the triangle into that bin; (3) compute the smallest axis-aligned bounding volume for each bin by iterating over all the binned triangles. When you have done this, you'll have a set of rectangular volumes that are probably a little bigger than the initial cubes, so they overlap a little bit. Pathologically large triangles might cause the bounding volumes to overlap significantly, but you can easily subdivide those triangles to eliminate the problem.

Which of these methods, clipping or binning, should we implement? Clipping increases the total triangle count, which should be cause for concern. I chose clipping anyway, though. The reason: even though non-overlapping bounding boxes were not a basic algorithmic requirement, they provide a greater interoperability with arbitrary rendering algorithms. Some algorithms require a strict rendering order for correctness, such as rendering back-to-front. If we're rendering grid squares that don't overlap, we can quickly achieve correct ordering of every triangle in the scene like this: (1) sort the triangles in each block individually; (2) treating each block as an indivisible unit, sort the blocks by the distance from their center points to the camera; (3) render the blocks in the sorted order.

This sorting works because the grid squares are regions of space that result when you chop the space up with a bunch of planes. The applicable idea here is "render everything on the same side of a plane as the viewpoint, then everything on the opposite side", which is the same idea that makes BSP tree visibility work. A grid of cubes is isomorphic to a BSP tree; it's just stored in array form instead of tree form (and array form has a lot of advantages!)

Now it's true that one of the basic goals of this algorithm is to enable the treatment of blocks as opaque entities, so that we can run very quickly; if we need to sort the blocks, we lose much of that speed. But the user of the LOD algorithm should ideally be free to make that judgement call himself: whether to adopt an order-dependent rendering algorithm and accept slower running, or whether to run with unsorted blocks, getting higher triangle throughput, and using a different shading algorithm. If we don't clip, we make it much harder to properly sort the scene; we are effectively saying "if you use this LOD algorithm, you won't be able to do rendering techniques X, Y, or Z without undue pain".

In fact we saw an order-dependent rendering technique last month: the color blending method of interpolating between LODs, used on DirectX8 and earlier hardware. Rather than sorting the triangles in each block, though, the algorithm used the Z-buffer to effectively sort on a per-pixel level. This color-blending technique already tolerated some inaccuracy in order to run quickly: occluded triangles in the translucent layer for a block may or may not contribute color to the rendered scene, depending on the order the triangles are stored in the mesh. However, due to the way colors were being blended, the inaccuracies are small and hard to notice. I suspect that if we used binning, and thus rendered the scene slightly more out-of-order, the resulting errors would be similarly subtle, and the result would be acceptable. Just the same, though, one of my major goals has been to make the system maximally compatible with unforeseen game engine components. It seems like strict ordering is a potential trouble spot for cross-algorithm interactions, so I chose clipping.

Then again, maybe the set of conflicting rendering techniques is small and unimportant. If we decide not to support them, we get a simpler LOD system, because binning is simpler than clipping. A simpler LOD system is desirable so that when the user needs to modify it, his job will be easier. Really, this is a tough call to make.

Another reason I chose clipping in the end was that, with regard to seam-building, clipping is a superset of binning: you need to solve the weird cases that happen with binning, and do extra work on top of that to clip. So a clipping solution illustrates both cases, and if you wanted to simplify the preprocessing stage to use only binning, you can streamline the sample code instead of writing something from scratch.


Clipping and Triangle Count

The extra triangles created by clipping may not matter much. When we give the block to our mesh simplifier -- assuming the simplifier works effectively -- these triangles will mostly be seamlessly merged, so they'll have a small impact on the resulting triangle count and topology. So the time the extra triangles should matter most is in the highest-resolution blocks.

On fast modern hardware, when geomtery is finely tessellated, a relatively small number of triangles are created by clipping. To show why, let's once again look at a mesh built from a square grid of vertices. The number of triangles in the block is 2n², where n is the number of samples on each side of the block. But the number of triangles added by clipping is approximately 4n. So as we increase the resolution of our world mesh, the number of triangles added by clipping grows much more slowly than the number of triangles we actually render.


Building Seams

With seams we follow the same basic strategy presented last month: create seams between the meshes at the highest resolution, then cross-reference them into the reduced meshes. This gives us fully precomputed seams that can be rendered quickly.

For every line segment produced by clipping, we must create a degenerate quad to bridge any potential gap (Figure 2). Because we're working in 3D now, we have the possibility that one of these segments will lie on a border between more than two blocks. If we employ an algorithm that generates seams between blocks based on which planes the segment touches, we could generate strange spurious seam triangles in this case.

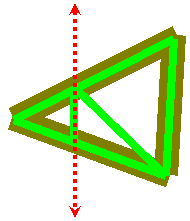
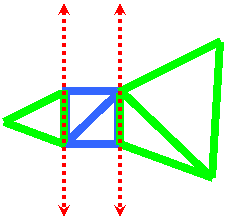
Figure 2a: A triangle (brown) has been clipped by a plane (red dashed line).  The resulting convex polygons must be triangulated, yielding three triangles in this case (green).	Figure 2b: We insert a degenerate quad (blue) to link the triangles on each half of the plane. The triangles have been artificially pulled apart here so that the quad is visible.

There are other things we need to worry about, too. When clipping geometry by a plane, we usually classify vertices as being in the plane's positive halfspace, or being in the negative halfspace, or lying on the plane. We can end up in a situation where two connected triangles straddle the plane (Figure 3). Even though clipping doesn't create new geometry in this case, we need to detect it and add the appropriate seam.
 

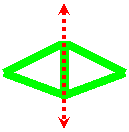Figure 3: Two triangles straddle the clipping plane.

In the sample code I wanted to solve all this while trying to keep things simple. The approach I take is to clip each block in isolation, then match up seams between the blocks after the clipping phase is complete. Whenever I create a new edge via clipping, or detect an edge coplanar to one of the clipping planes, I add it to a list of potential seam edges. When all the blocks are clipped, I look at neighboring blocks and match up edges, creating degenerate seam quads between them. This two-pass approach is also important for out of core clipping, which may be necessary for large input geometry; so it's good to have it already built into the core algorithm.

When matching up the seam edges between blocks, we need to ensure that we don't attach the wrong edges to each other. There might be ambiguity due to multiple vertices located in the same positions, or due to floating-point calculations coming out slightly differently when edges are clipped multiple times. (Ideally such floating-point problems don't happen if you're careful in the code that computes clipped coordinates; but the current state of FPU management in Windows game software is dicey so extra care is warranted.) To eliminate all ambiguity, I identify each edge by its two endpoint vertices; each of those vertices is identified by three integers: the two indices of the vertices in the input mesh that comprised the segment that was clipped to yield this vertex, and the index of the clipping plane that clipped that segment. If the preceding sentence is difficult to decipher, the details aren't so important; the basic idea is that we have a unique integer method of identifying each clipped edge, and we don't rely at all on the floating-point output of the clipping system to match them up.

Remember last month we saw that, in the heightfield case, holes will appear in the mesh between the corners of blocks at varying LODs. An analogous problem happens in 3D, and we need to analyze that. Also, we haven't discussed methods of deciding which LOD of a given block to render. We'll get to both of those next month.