The Inner Product, June 2003
Jonathan Blow (jon@number-none.com)
Last updated 16 January 2004
 

Unified Rendering Level-of-Detail, Part 4

Related articles:

Rendering Level-of-Detail Forecast (August 2002)
Unified Rendering LOD, Part 1 (March 2003)
Unified Rendering LOD, Part 2 (April 2003)
Unified Rendering LOD, Part 3 (May 2003)
Unified Rendering LOD, Part 5 (July 2003)

Note: This article is currently missing Figure 2. 
We will attempt to remedy this situation in the future.

In this series of articles we're working on a renderer that can display large triangle soup environments. We accomplish this by dividing the environment into chunks, then creating reduced-detail versions of the chunks, ensuring that no cracks are introduced in the process of detail reduction.

Last month we clipped a triangle soup into two pieces, connecting the pieces with some filler triangles that I called a "seam". We created reduced-detail versions of each half of the input mesh, ensuring that the seam triangles always preserved the manifold between the halves. Now we will extend this clipping method to an arbitrary number of pieces. Then we will be able to render an LOD'd triangle soup using the chunk selection and blending system discussed in parts 1 and 2 of this series (back then, the system was used only on height fields).


Multiple Clipping Planes

Last month's system only used one clipping plane. You might think that we could just apply that method repeatedly to chop up the input mesh, and be done. But some complications arise, which we will look at now.

With only one clipping plane, we create only two chunks of geometry. Computing the seam between these two chunks is relatively straightforward, as we saw last month: first we construct a seam between the chunks at the highest resolution, then we incrementally generate reduced-resolution versions of that seam using information returned by the detail reducer.

This method produces manifold-preserving seams between any two chunks of geometry. Recall that in the height-field system we stored 3 seams for each block and each direction. There were 3 seams because neighboring blocks were permitted to differ by one level of resolution, and we needed to handle each combination: whether a neighbor is one level lower in detail, at equal deail, or whether there were two neighbors one level higher.

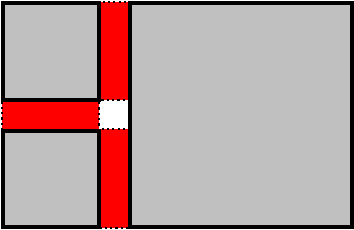
We mentioned that, when multiple chunks of geometry neighbor each other, filling the gaps between each pair of chunks is not enough. In corners where multiple chunks meet, we can have a "pinhole" (Figure 1). With a height field, we might fill these holes by marking the corner vertices of each block at preprocess time, and at runtime drawing two triangles between these vertices.
 

Figure 1: Three terrain blocks (gray with black borders) and the seam fills between them (red with dotted borders). Note the hole in the middle. These blocks are drawn with exaggerated gaps; the actual hole would be very small.

But imagine trying to extend this strategy to a 3D grid of chunks. Now there are two major ways that multiple chunks meet: along cube edges, where four chunks can meet, as in the 2D case; and also at cube corners, where eight chunks can meet. It becomes difficult to see a way that holes can be dynamically filled, because there is no longer a coherent concept of "corner vertices" to each block. A cube edge that passes through a mesh can create many "corner vertices" and some of these may disappear as the chunk's resolution is adjusted. If a coherent dynamic solution exists, it is messy and probably slow. (The seam-drawing code for the heightfield system already contained an unsavory amount of confusing code that performs tree-traversal-to-find-neighbors, and I'd hate to exacerbate that situation).

So instead of filling the holes dynamically at runtime, we can seek a preprocess-oriented solution. At the highest level of LOD, when we first create chunks by splitting up the triangle soup, it is probably not difficult to correctly fill the pinholes. Then we create reduced-detail seams, as before. The situation is messier because we have to deal with more neighbors in more directions; also a seam can now touch multiple blocks, and planning out data structures to handle the resulting combinatorics can be a big headache. But in principle it can be done.


Increased Combinatorics

However, the situation becomes messier when we realize that in 3D, we probably can't impose the constraint that two fully diagonal neighbors must always be within 1 detail level. We have a choice of two major methods to impose this constraint. The first is by implementing a Lindstrom-Koller style dependency system, wherein some chunks can force other chunks up to higher levels of detail. However, for many choices of chunk size and precomputed chunk resolution, the chunks will naturally want to decrease by more than one resolution per step as you move away from the camera. In such cases, the dependencies will force chunks to higher resolutions than they want to be, in an effect that ripples across the entire environment. The end result is that your scene contains a lot more triangles than you want, which is something to avoid.

We also want to avoid such a scheme because it complicates the runtime algorithm. So we can take the alternative approach. We design the LOD selection system so that neighboring chunks, when evaluated in isolation, always happen to be chosen in such a way that the constraint holds. (This is the method that has been used in the heightfield renderer so far.) We accomplish this by ensuring at preprocess time that the isosurfaces of the LOD decision functions are always appropriately nested; we'll talk about this next month. In this case we get a similar ripple effect, but it happens at preprocess time instead of runtime. The end result is that we again waste triangles.

So, to fix this, we must give up the 1-level-neighbor constraint. That means the combinatorics between neighboring detail levels can grow much larger. We need to build seams that tie together chunks that are 2 or 3 levels apart.

When I first thought about how to program this system, I envisioned an octree containing all the chunks. To build a seam between some high-res blocks and their low-res neighbor, I would collapse one level of the octree in the appropriate place, cross-reference the high-res seams, to build a new seam, and record that result. This process can be applied repeatedly until we exhaust all the combinations; but programming all this is still a headache. (First we need to collapse portions of the octree by one level, choosing them one at a time, then two at a time, then three at a time, et cetera; then we need to collapse one portion of the octree by two levels, but the rest of them by only one level, repeating all the previous combinations; then two portions by two levels, etc. It just feels nasty, and it would require a lot of the unhappy neighbor-navigation code mentioned above.)

I was unsatisfied with this solution. I wanted a way to deal with all these combinations that was easy to program and easy to understand, so I can put this LOD manager in the core of my rendering system and have some confidence that it actually works.


Triangle-Centricity

Happily, I managed to come up with a simpler system to do all this. Two main observations helped me find the simplifications. Both observations came about when I decided to stop thinking about octrees and chunk borders and seams, and moved to an entirely triangle-centric viewpoint.

The first thing I realized was that any triangle, having only 3 vertices, can only touch at most 3 chunks simultaneously. Thus, if we ever do anything that cares about the combinatorics of more than 3 blocks at once, whether at preprocess time or at runtime, that's a sign that we're complicating the situation needlessly.

The second useful observation was that, when remapping the high-res seams, we don't actually need much information about which chunks neighbor which others. We only need to know which chunks contribute to which lower-resolution chunks; then we can use that information to _rewrite_ existing seam triangles, and we get all the combinatorics for free.


A Database of Seams

We can think of each triangle as being a triplet of "vertex specifiers"; each specifier tells us which chunk of geometry, and which index inside that chunk, represents the vertex we want. Suppose we have some chunk named A. The vertex specifier for chunk A, index 7 can be written as "A7". A seam triangle connecting chunks A and B might be written as (A7, B10, A8).

Suppose we detail-reduce chunk B into a new chunk C, and vertex 10 of B becomes vertex 3 of C. To help create the corresponding seam, we want to rewrite the above triangle so that it becomes (A7, C3, A8). As long as we perform this step properly for every triangle that contains B in a vertex specifier, we will successfully preserve the manifold. It doesn't matter who the neighbors of A, B, and C happen to be. The fact that seams always tie neighbors together becomes an inductive property, caused by the fact that we only made seams between high-res neighbors to begin with. We don't need to worry about maintaining this property between resolutions, because it happens automatically.

At preprocess time, I maintain a database of all existing seam triangles. First I split input geometry into chunks and put the resulting high-res seams into this database. Then I perform the detail reductions, and for each reduction I execute a _rewrite rule_ on the database. The rewrite rule just searches for all triangles containing a certain chunk in their specifiers, writes new versions of those triangles with the new chunks and indices (such as the B10-to-C3 conversion above), and adds the new triangle to the database. We repeat this process, always adding new triangles to the database, never removing any.

By the time we've reduced our input geometry to a single low-resolution chunk, the database has computed for us all combinations of all seams between neighbors of all possible resolutions. (To get a feel for this, try it with a simple case on pencil and paper!)

We may not wish to store all these combinations, so we can impose limits; for example, we can tell the database never to create seams between chunks that differ by more than 2 or 3 levels of detail. We can even set this limit on a case-by-case basis, with those decisions arising from an analysis of the input geometry.

I have spoken here of manipulating individual triangles; but in the implementation, to reduce memory and CPU costs, I group the triangles into seams as before, with the grouping based on the chunk part of their vertex specifiers. So the "chunk membership" is stored in an array on the seam and used for all triangles within the seam; only the vertex indices are stored per-triangle.

All this makes the preprocessing solution rather tidy. But how do we organize these seams so they can be found quickly at runtime? The high-level answer to this is that we just store the seam database wholesale and reload it for runtime use. To draw seams between all the solid-rendered chunks on the screen, we first make an array of those chunks (which we already did so that we could render them!), then just tell the database "give me all the seams that only touch blocks in this set". Then render those seams. Simple, easy, done.

Now, "database" is a scary word for engine programmers who are trying to do fast graphics. One might have nightmarish visions of SQL queries happening inside the render loop. In actuality, since the number of specific queries we want to do at runtime is very small (perhaps we only need the query mentioned above), we can set up data structures that help us answer those queries quickly. But to maintain simplicity, I think it's important to consider this as a problem of "accelerate a database query about vertex specifiers", and not fall into the mentality of "store seams in arrays based on neighbors and resolutions" as we did with the heightfield renderer.

In this month's sample code, the seams are stored in the database in a single linear array, and I perform the database query as follows. First I mark all the chunks that are being rendered. Then I iterate over every seam in the database, and check the chunks it touches (of which, remember, there can be no more than 3). If all the chunks are marked, I render the seam, otherwise I don't. After this is done, I unmark all the marked chunks.

This algorithm is O(m) where m is the total number of seams in the database. That's fast enough for the data sizes we are dealing with now, but in a big system it might be a little bit slow. But by storing seams in arrays on each chunk (which any seam being referenced by multiple arrays), we can reduce the running time to O(n) where n is the actual number of seams you need to draw. Since the task rendering the seams, itself, is O(n), it wouldn't help us much to try and drive the running time lower. Perhaps I will implement this version of the query next month.


The Moral of the Story

I think there's a moral to this database thing that I would like to remember. There's a certain set of concepts and data structures (like octrees) that we, as engine programmers, are used to thinking about. When approaching a new problem, we tend to apply these concepts first, perhaps not seeing other ways of thinking about the situation. But even though those data structures have helped us in the past, they may not help us now; in fact they may serve only to confuse matters. I am reminded of that silly proverb "when all you have is a hammer, everything looks like a nail".


Increased Freedom

Now that we use this database rewrite system, neither the preprocess nor the rendering requires an octree. In fact they require very little in the way of data structures. We need only a set of hierarchical bounding volumes for frustum culling and some LOD metric we can apply to each chunk. That's an amazing amount of freedom, much more than I envisioned when I started this project. That freedom is good; it means anyone using the algorithm will not have many restrictions in how this system must interact with the rest of their renderer.

In fact, nothing in this entire algorithm even cares about the dimensionality of the space we are working in. So if you are some kind of weird physicist running simulations in 11 dimensions and you need a system to perform LOD for you, maybe this will be suitable.

Given this newfound freedom, I'm going to try something different than I originally planned. Instead of using a 3D grid of blocks to store the seam, I will employ a system of BSP-style cutting planes, situated at arbitrary orientations. I will compute these cutting planes based on the density of the scene.


Filling Pinholes

The seam database approach worked so well for LOD generation that I used it for the initial chunk generation as well. I split a chunk into sub-chunks by applying a single splitting plane and rewriting the seams in the database. Often this will split a seam into two, adding also a single-triangle pinhole filling seam, as seen in Figure 2. This correctly preserves the manifold for one split; and thus, since we perform one split at a time, inductively it preserves the manifold until we've got all our chunks and are ready to build LODs.

This month's sample code contains two different running systems. One of them is the heightfield renderer, modified to use the seam database approach. This serves as a relatively simple introduction to the database, as it doesn't need any of the chunk splitting mentioned above (a heightfield can be chunked just by applying a window to the array of data).

The second system in the sample code is a new version of the bunny chopping program, modified now to use an arbitrary number of splitting planes. This program serves as an illustration of the BSP-style cutting planes I am talking about, and it serves to verify that the mesh chunking and pinhole-filling schemes work properly. You can see the results in Figure 3.

Next month we'll look at LOD metrics, discuss methods of choosing splitting planes, and generally finish things up.

Figure 3 3a (upper left): The Stanford Bunny, chopped into arbitrary chunks by four different splitting planes. The original mesh contained 16000 triangles, but the portion in the upper-right has been reduced by one level of detail. The seam-filling triangles have been drawn in red, and the pieces of the bunny have been pulled apart so that you can see the seams. 3b (upper right): The same geometry as 3a, but rendered more like it would be in an actual game, without the pieces pulled apart.  3c (lower left): Like 3a, but now we have reduced the left half of the mesh by three levels of detail. Note that the seams are still properly filled.  3d (lower right): Like 3c, but without the pieces pulled apart.